Bijectors#
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from rlxutils import subplots, copy_func
import tensorflow_probability as tfp
import tensorflow as tf
import ppdl
import pandas as pd
tfd = tfp.distributions
tfb = tfp.bijectors
%matplotlib inline
Bijectors are invertible transformations#
When applied to TFP distributions bijectors produce fully valid distributions
TFP has a collection of Bijectors that allow you to transform distributions, keeping the capability for sampling and compute densities.
We will see them more in detail later in the course, but for now, let’s understand what they do.
Observe how we scale and shift a distribution.
bscale = tfb.Scale(.5)
bshift = tfb.Shift(.3)
d_orig = tfd.Beta(1.8,1.5)
d_scaled = bscale(d_orig)
d_scaled_and_shifted = bshift(d_scaled)
for ax,i in subplots(range(3), usizex=5):
if i==0: ppdl.plot_pdf(d_orig); plt.title("original")
if i==1: ppdl.plot_pdf(d_scaled); plt.title("scaled")
if i==2: ppdl.plot_pdf(d_scaled_and_shifted); plt.title("scaled and shifted")
plt.xlim(-.1,1.1)
plt.grid();
plt.tight_layout()

the resulting distribution are fully valid TFP distribution objects
d_scaled
<tfp.distributions.TransformedDistribution 'scaleBeta' batch_shape=[] event_shape=[] dtype=float32>
s = d_scaled.sample(10)
s
<tf.Tensor: shape=(10,), dtype=float32, numpy=
array([0.11156841, 0.39035392, 0.07765947, 0.19926141, 0.3500817 ,
0.19258274, 0.16098109, 0.31810397, 0.10686599, 0.09793448],
dtype=float32)>
d_scaled.log_prob(s)
<tf.Tensor: shape=(10,), dtype=float32, numpy=
array([0.5458902 , 0.91539323, 0.29789424, 0.8819361 , 0.9846997 ,
0.86564505, 0.77117884, 1.0047415 , 0.5174571 , 0.4588679 ],
dtype=float32)>
Chaining and inveting bijectors#
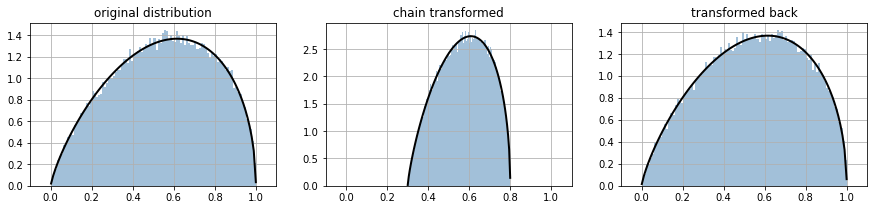
you can chain bijectors to crete a new bijector. Observe that they are specied in inverse order to which they are applied.
you can also create an inverse bijector.
bc = tfb.Chain([bshift,bscale])
bci = tfb.Invert(bc)
dt = bc(d_orig)
d_back = bci(dt)
for ax,i in subplots(3, usizex=5):
if i==0: ppdl.plot_pdf(d_orig); plt.title("original distribution")
if i==1: ppdl.plot_pdf(dt); plt.title("chain transformed")
if i==2: ppdl.plot_pdf(d_back); plt.title("transformed back")
plt.xlim(-.1,1.1)
plt.grid();
Bijector are general transformations on TF objects#
x = tf.Variable(2.)
tx = bc(x)
tx
<tf.Tensor: shape=(), dtype=float32, numpy=1.3>
bc.inverse(tx)
<tf.Tensor: shape=(), dtype=float32, numpy=2.0>
Modelling stuff#
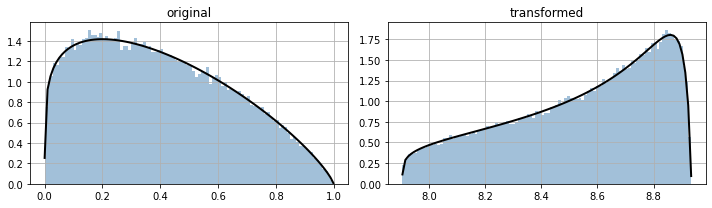
bijectors make it easier to model stuff with non standard distributions, for instance
t = tfb.Chain([tfb.Scale(3), tfb.Shift(2), tfb.Tanh(), tfb.Scale(1.5), tfb.Shift(+.5)])
d1 = tfd.Beta(1.2,1.8)
d2 = t(d1)
for ax,i in subplots(2, usizex=5):
if i==0: ppdl.plot_pdf(d1); plt.title("original")
if i==1: ppdl.plot_pdf(d2); plt.title("transformed")
plt.grid();
plt.tight_layout()
validate_args#
Observe that sometimes a bijector might not be invertible for certain input values.
This is only checked in validate_args is set to True, otherwise, nan are generated and the code downstream will fail somewhere
t = tfb.Square()
d = tfd.Normal(loc=0, scale=1)
dt = t(d)
s = dt.sample(10)
s
<tf.Tensor: shape=(10,), dtype=float32, numpy=
array([0.05243969, 0.00711866, 0.3022964 , 0.08465093, 1.0127188 ,
1.7130485 , 0.5749669 , 0.41861057, 0.9270925 , 0.80052745],
dtype=float32)>
dt.prob(s)
<tf.Tensor: shape=(10,), dtype=float32, numpy=
array([0.84852153, 2.3557818 , nan, 0.6571772 , 0.1194611 ,
0.06471597, 0.19733593, nan, nan, nan],
dtype=float32)>
with validate_args set to True an exception is rised and can be dealt with
t = tfb.Square(validate_args=True)
d = tfd.Normal(loc=0, scale=1)
dt = t(d)
try:
s = dt.sample(10)
except Exception as e:
print (e)
All elements must be non-negative..
Condition x >= 0 did not hold element-wise:
x (shape=(10,) dtype=float32) =
['-0.9586899', '0.72535914', '1.2406634', '...']
but the code is slower even for a simple scenario. We test both cases with positive samples which we know are valid
t = tfb.Chain([tfb.Scale(2, validate_args=True), tfb.Square(validate_args=True)])
d = tfd.Normal(loc=100, scale=1)
dt = t(d)
%timeit s = dt.sample(1000)
%timeit dt.log_prob(s)
3.12 ms ± 34 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
9.94 ms ± 252 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
t = tfb.Square()
t = tfb.Chain([tfb.Scale(2), tfb.Square()])
d = tfd.Normal(loc=100, scale=1)
dt = t(d)
%timeit s = dt.sample(1000)
%timeit dt.log_prob(s)
2.92 ms ± 52.5 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
8.89 ms ± 413 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
Bijector parameters are learnable#
observe how we can learn altogether bijector and distribution parameters
scale = tfb.Scale(3)
a,b = 2, 1.5
dbeta = tfd.Beta(a,b)
d_orig = scale(dbeta)
x = d_orig.sample(100000)
ppdl.plot_pdf(d_orig, hist_args={'color': 'red', 'bins': 100, 'alpha': .5})
plt.axvline(np.mean(x), ls="--", color="black", alpha=.5, label="sample mean")
plt.grid(); plt.legend();
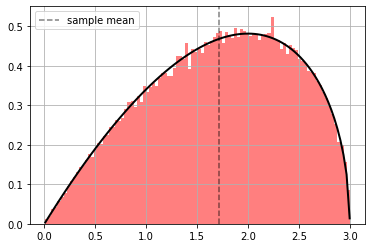
Although trivial, we will just learn the bijector parameter.
def optimize(init_sc=10., validate_args=False):
sc = tf.Variable(init_sc, dtype=tf.float32)
optimizer = tf.keras.optimizers.Adam(learning_rate=0.1)
hloss = []
hgrads = []
hparams = []
for epoch in pbar(range(200)):
with tf.GradientTape() as tape:
c = tfb.Scale(sc)
d = c(tfd.Beta(a,b, validate_args=validate_args))
negloglik = -tf.reduce_mean(d.log_prob(x))
hloss.append(negloglik.numpy())
gradients = tape.gradient(negloglik, [sc])
if np.any([np.isnan(i) for i in gradients]):
print("nan gradients")
break
optimizer.apply_gradients(zip(gradients,[sc]))
hgrads.append(gradients)
hparams.append(sc.numpy())
hgrads = np.r_[hgrads]
hloss = np.r_[hloss]
hparams = np.r_[hparams]
return hloss, hparams, hgrads, sc
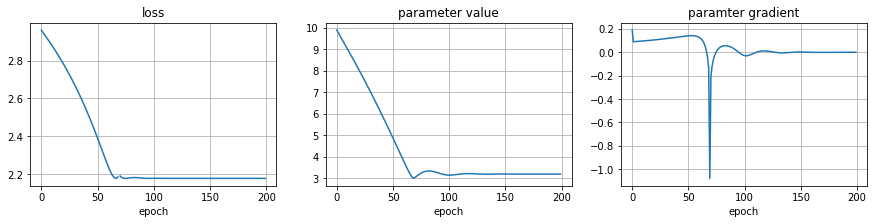
def plot_optim(hloss, hparams, hgrads):
for ax,i in subplots(3, usizex=5):
if i==0: plt.plot(hloss); plt.title("loss")
if i==1: plt.plot(hparams); plt.title("parameter value")
if i==2: plt.plot(hgrads[:,0]); plt.title("paramter gradient")
plt.xlabel("epoch")
plt.grid();
hloss, hparams, hgrads, sc = optimize()
sc
100% (200 of 200) |######################| Elapsed Time: 0:00:03 Time: 0:00:03
<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=3.1905434>
plot_optim(hloss, hparams, hgrads)
ppdl.plot_pdf(d, hist_args={'label': 'fitted distribution', 'bins': 100, 'alpha': .5})
plt.hist(x.numpy(), bins=100, density=True, alpha=.5, color="red", label="original distribution")
plt.grid(); plt.legend();
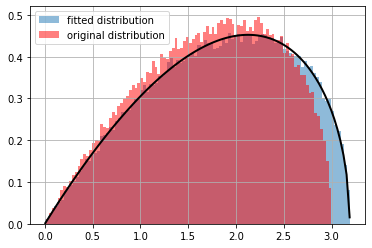
observe that we might hit invalid values during optimization. The Beta distribution returns nan if trying to compute densities for values outside its domain.
hloss, hparams, hgrads, sc = optimize(init_sc=-5)
75% (150 of 200) |################ | Elapsed Time: 0:00:02 ETA: 0:00:00
nan gradients
plot_optim(hloss, hparams, hgrads)
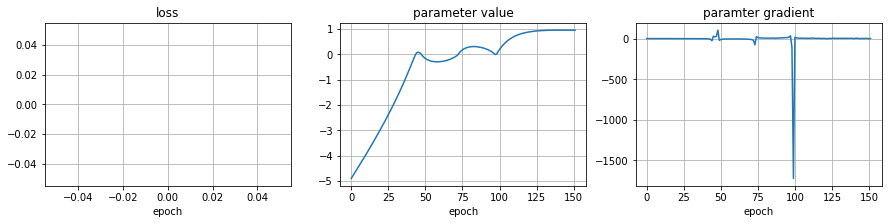
with validate_args set to True TFP checks stuff and will hint these situations
hloss, hparams, hgrads, sc = optimize(init_sc=-5, validate_args=True)
0% (0 of 200) | | Elapsed Time: 0:00:00 ETA: --:--:--
---------------------------------------------------------------------------
InvalidArgumentError Traceback (most recent call last)
/tmp/ipykernel_53908/1940918081.py in <module>
----> 1 hloss, hparams, hgrads, sc = optimize(init_sc=-5, validate_args=True)
/tmp/ipykernel_53908/734260892.py in optimize(init_sc, validate_args)
13 c = tfb.Scale(sc)
14 d = c(tfd.Beta(a,b, validate_args=validate_args))
---> 15 negloglik = -tf.reduce_mean(d.log_prob(x))
16 hloss.append(negloglik.numpy())
17
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow_probability/python/distributions/distribution.py in log_prob(self, value, name, **kwargs)
1314 values of type `self.dtype`.
1315 """
-> 1316 return self._call_log_prob(value, name, **kwargs)
1317
1318 def _call_prob(self, value, name, **kwargs):
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow_probability/python/distributions/distribution.py in _call_log_prob(self, value, name, **kwargs)
1296 with self._name_and_control_scope(name, value, kwargs):
1297 if hasattr(self, '_log_prob'):
-> 1298 return self._log_prob(value, **kwargs)
1299 if hasattr(self, '_prob'):
1300 return tf.math.log(self._prob(value, **kwargs))
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow_probability/python/distributions/transformed_distribution.py in _log_prob(self, y, **kwargs)
368 y, event_ndims=event_ndims, **bijector_kwargs)
369 if self.bijector._is_injective: # pylint: disable=protected-access
--> 370 base_log_prob = self.distribution.log_prob(x, **distribution_kwargs)
371 return base_log_prob + tf.cast(ildj, base_log_prob.dtype)
372
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow_probability/python/distributions/distribution.py in log_prob(self, value, name, **kwargs)
1314 values of type `self.dtype`.
1315 """
-> 1316 return self._call_log_prob(value, name, **kwargs)
1317
1318 def _call_prob(self, value, name, **kwargs):
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow_probability/python/distributions/distribution.py in _call_log_prob(self, value, name, **kwargs)
1294 value, name='value', dtype_hint=self.dtype,
1295 allow_packing=True)
-> 1296 with self._name_and_control_scope(name, value, kwargs):
1297 if hasattr(self, '_log_prob'):
1298 return self._log_prob(value, **kwargs)
/opt/anaconda/envs/p39/lib/python3.9/contextlib.py in __enter__(self)
117 del self.args, self.kwds, self.func
118 try:
--> 119 return next(self.gen)
120 except StopIteration:
121 raise RuntimeError("generator didn't yield") from None
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow_probability/python/distributions/distribution.py in _name_and_control_scope(self, name, value, kwargs)
1995 deps.extend(self._parameter_control_dependencies(is_init=False))
1996 if value is not UNSET_VALUE:
-> 1997 deps.extend(self._sample_control_dependencies(
1998 value, **({} if kwargs is None else kwargs)))
1999 if not deps:
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow_probability/python/distributions/beta.py in _sample_control_dependencies(self, x)
335 if not self.validate_args:
336 return assertions
--> 337 assertions.append(assert_util.assert_non_negative(
338 x, message='Sample must be non-negative.'))
339 assertions.append(assert_util.assert_less_equal(
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow/python/util/traceback_utils.py in error_handler(*args, **kwargs)
151 except Exception as e:
152 filtered_tb = _process_traceback_frames(e.__traceback__)
--> 153 raise e.with_traceback(filtered_tb) from None
154 finally:
155 del filtered_tb
/opt/anaconda/envs/p39/lib/python3.9/site-packages/tensorflow/python/ops/check_ops.py in _binary_assert(sym, opname, op_func, static_func, x, y, data, summarize, message, name)
407 data = [message] + list(data)
408
--> 409 raise errors.InvalidArgumentError(
410 node_def=None,
411 op=None,
InvalidArgumentError: Sample must be non-negative..
Condition x >= 0 did not hold element-wise:
x (shape=(100000,) dtype=float32) =
['-0.44549665', '-0.05629177', '-0.39321715', '...']

